Alice and Bob
An example of how traditional grades misrepresent learning

We’ve written a lot about how traditional grades aren’t mathematically valid (and how sometimes a number isn’t a number). In short, it doesn’t make mathematical sense to add and average grades in the way often done in a traditional grading system.
That might get too deep into the mathematical weeds for some.1 So when I give talks about alternative grading, I often begin with a concrete example to illustrate how traditional grades can badly misrepresent student learning. I’ve never put this up on the blog, so today I’ll remedy that.
Let’s meet our protagonists:
Alice and Bob
Alice and Bob2 are students in a class that uses traditional weighted average grading, the sort that every LMS is set up to use by default.
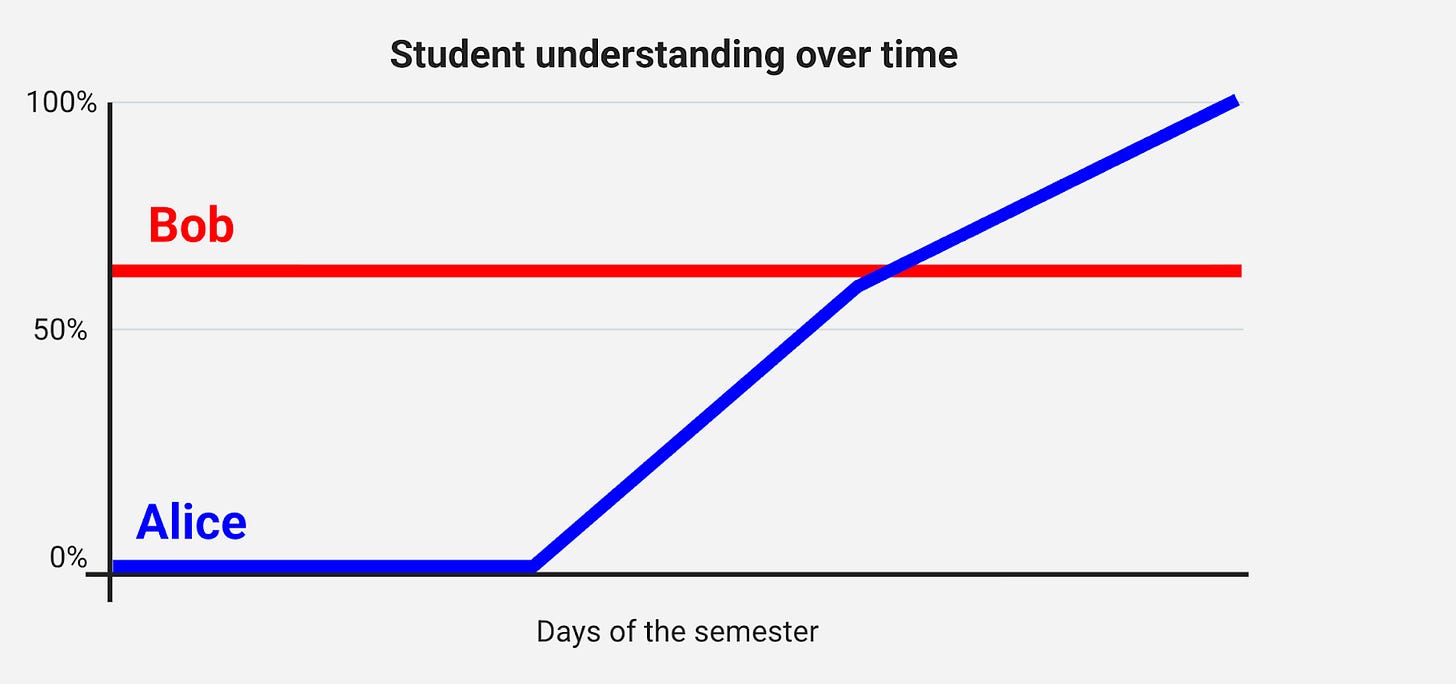
Here’s a picture to illustrate their overall progress in understanding the course material throughout the semester:
Let’s begin by taking a look at this (very abstracted) picture. What do you notice about it? What do you wonder – about the students, their progress, the class…?
Take a moment to do that now.
Here are some things I usually hear:
Alice really showed improvement, while Bob didn’t improve at all.
What happened at the start for Alice? Was she missing classes? Test anxiety? Didn’t understand? What changed?
Did Alice cheat?
Did Bob really learn anything in the class? Was he getting by on partial credit?
Let’s assume for the sake of argument that this is an accurate picture. If you had to assign Alice and Bob letter grades based only on this picture, what grade might you assign, and why?
Take a second to do that now.
Of course, we don’t assign grades based only on vibes (this is a good thing). So let’s look at how grades are assigned in this specific class. Alice and Bob’s traditionally graded class also has pretty traditional assessments: Two midterm exams (each worth 25%) and a cumulative final exam (worth 50%).
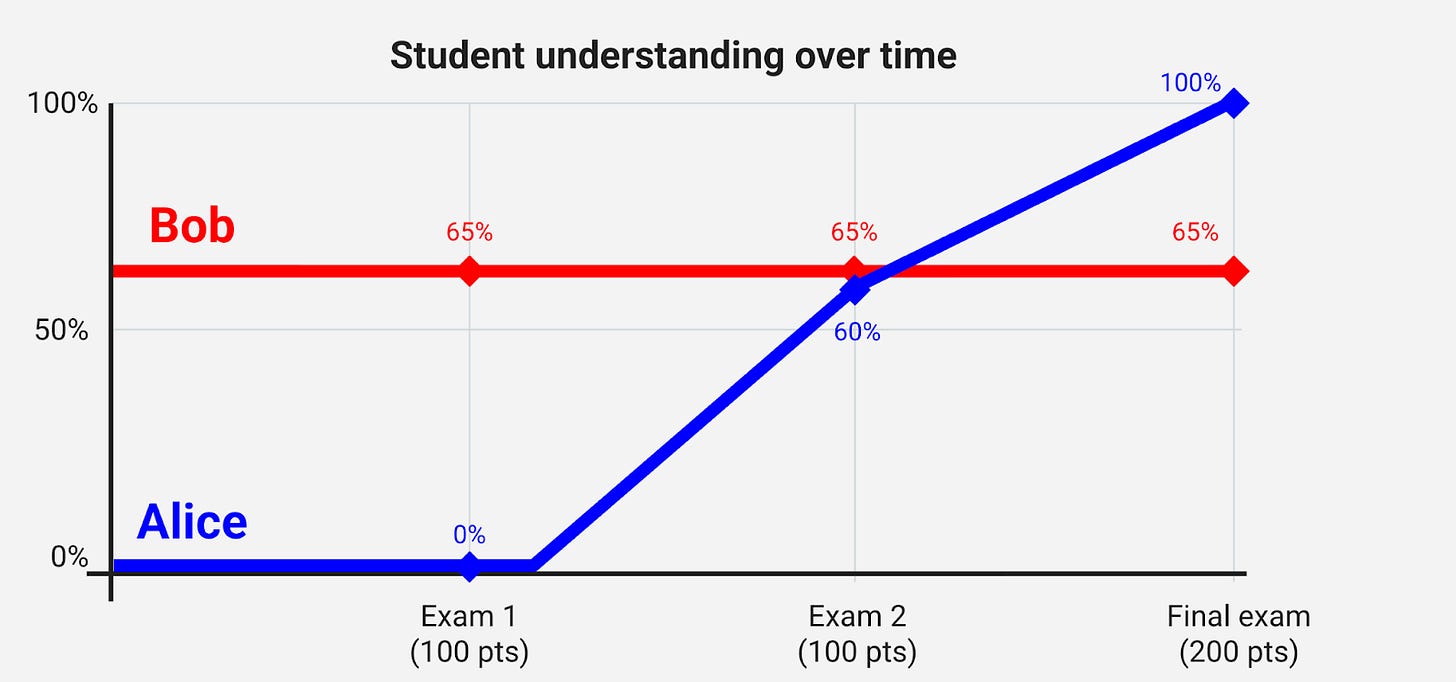
The thing about assignments like these is that they check in on a student’s learning at a specific point in time, and then permanently record that progress as if it were an unchanging truth. Here are Alice and Bob’s grades on each of those exams:
Here’s an equivalent way to view this data in terms of points:
And here’s what that looks like on the graph:
Now that we have numbers, we can calculate a final grade. This is a standard weighted calculation: Take the student’s grade on each exam, multiply it by that exam’s weight, and add it all up. So in this case, Alice gets:
(25% ⨉ 0) + (25% ⨉ 60) + (50% ⨉ 100) = 65
Alice’s final grade is 65%, or about a D on most scales.
Likewise, we can do the same with Bob, which isn’t a tricky calculation. He gets:
(25% ⨉ 65) + (25% ⨉ 65) + (50% ⨉ 65) = 65
… also 65%, about a D.
Alice and Bob, despite their very different trajectories, have earned exactly the same grade – one that, at most institutions, is barely (if at all) passing.
Does this line up with the grades you chose for them at the start of this section? I doubt it. And that’s the point.
What Alice and Bob tell us about traditional grades
The grades in this class are completely hiding important differences between Alice and Bob. This example illustrates a few important things about traditional grades:
Averaging penalizes the learning process. Alice learned something in the class, and by the end she was showing full understanding. Bob, well… didn’t. But the grading system in their class permanently averaged in Alice’s early struggles as well as her later successes. That means that Alice is permanently penalized for having a rough start. Even when Alice does exactly what we want students to do – persist, work hard, and eventually come to full understanding – there’s no way to remove the effect of those initial low grades (remember, that final exam is cumulative!). In fact, after the first exam, Alice couldn’t earn higher than a 75% final grade in the class. She was mathematically eliminated from an A or B. This is what I mean by “penalizing learning”: A student who does the very human thing of engaging with a feedback loop to improve and learn is penalized for needing to do exactly that. You could think of this as a “false negative”: The grading system is indicating that Alice understands less than she actually does.
Alternative grading addresses this through reattempts without penalty. The without penalty part is essential, and it’s what would help Alice the most. A student who can eventually demonstrate understanding of a topic doesn’t have to worry about earlier attempts weighing them down, because a grade that represents their ultimate level of understanding replaces any grade that represents their earlier attempts.
Partial credit sets low standards. This might be what we’re seeing with Bob. Both partial credit and averaging give Bob a chance to “get by” without demonstrating full understanding of any topic. This sets low expectations: A weighted averaging system tells students that they can pass the class by playing the numbers and getting by on partial credit, rather than focusing on actually learning. You could view this as a “false positive”, where the grade says that Bob understands more than he actually knows.
Alternative grading changes this in two key ways. First, marks that indicate progress do away with partial credit. Ultimately a student earns credit for consistently demonstrating relevant evidence of learning without important errors. This is a very high standard that requires students to show real learning. Second, by setting grade requirements in terms of clearly defined standards, grades are more clearly linked to specific learning rather than being a game of numbers.
Numerical grades are “objectivity theater.” There’s an old saying that “the numbers don’t lie”. With traditional grading, they absolutely do. Traditional grading hides the flaws I’ve described above behind a veneer of mathematical legitimacy. It’s easy to view numbers and formulas as objective and factual. Just look at the sample calculations I did above: You can check for yourself that the calculations are 100% correct. The truth is that this is “objectivity theater”: The numbers and formulas of traditional grades are created and assigned by humans, and humans can (and do) choose to do things with numbers that make no mathematical sense at all. I won’t rehash this fully, so if you haven’t seen it before, please check out that previous link as well as this one: Traditional Grades are Not Objective.
I’m not going to claim that alternative grading is immune to objectivity theater. But the process of designing an alternative grading system tends to pull back the curtain and force you to think about the meaning of your choices: which standards matter enough to count in a final grade? What level of understanding is sufficient? Those kinds of questions remove the option to hide behind formulas and percentages.
Objections
This story of Alice and Bob is meant to illustrate some points about how traditional grades work, and I encourage you to take it in that spirit. But this is also a simplified example, and objections are easy to come by. Here are a few, and how I typically think about them:
This is way too simple to be realistic. I’ll often hear comments about how things would change for Alice or Bob if the weights were changed, more grade categories added, if they could earn participation or attendance or extra credit points, etc.3 That’s fundamentally about tinkering around the edges. The truth is that any system based on points, partial credit, and averaging is going to have similar issues. I could argue mathematically, but I think it’s easier to say this: Do Alice and Bob seem familiar? I bet they do, and that’s because anyone who’s used a traditional grading system has encountered these kinds of situations. They are an inherent part of traditional grading. Maybe not as cleanly as presented here, but again, this is a simplified example for the purpose of illustration.
Could Alice be cheating? Maybe? That’s a question about Alice’s behavior, not about how her grade is determined, which is what this post is about. If you have a student who you suspect is cheating, you probably have policies in place to address that, and that’s true regardless of the grading system. There are often similar (but less negatively-phrased) concerns about what caused Alice’s early struggles: Attendance? A language barrier? Test anxiety? Family obligations? If anything, these are strong reasons to have a forgiving late work policy that focuses on learning over compliance with arbitrary rules.
I allow students to make up 50% of previously lost points if they do better on the final exam. <trim 5 minutes of background and philosophizing here>4 So, doesn’t that show that traditional grades can be salvaged? This sure sounds like a small step towards alternative grading: Reattempts with a minor penalty. Awesome! Keep it up… for example, why penalize students at all if they are able to show full understanding eventually? (At this point we risk getting into some of the knee-jerk reactions that some people have to alternative grading, for example “there are no redos in the real world”. Rather than continuing this thread, I’ll simply point you toward that article.) I encourage anybody who’s thinking this way about their traditional grades to take another small step towards alternative grading too.
A final thought
This example with Alice and Bob shows how traditional grades can badly misrepresent student learning. There’s something more that we haven’t talked about: This traditional grading process can also be enormously discouraging. Imagine you’re Alice after that first exam. How do you feel? Are you likely to want to keep trying in this class, knowing that no matter what you do, you can’t earn above a 75% final grade? Even if you do your best, at most you’re trying to keep your head above water while fighting a losing battle against math. That has a real effect on students: See Robert’s Origin Story for just one example.
This story about Alice and Bob can act as motivation. These types of situations are familiar to many instructors. The next step is lean in to supporting human learning through a feedback loop via the four pillars of alternative grading.
One final note: This Alice and Bob example is like folklore in the alternative grading community. We included it in our book, but I’ve used it – and seen many others use it – for years before that. I have no clue where it originated. I don’t claim any particular ownership of this example, and you are welcome to use or modify it as you see fit.
Hey, we’re mathematicians!
These names are traditional placeholder names used in cryptography, usually along with “Eve the evil eavesdropper”.
There’s a lot to say about how participation, attendance, and extra credit illustrate “objectivity theater”. In a traditional grading system, a point for attendance, or for unrelated extra credit, counts exactly the same as a point for showing real understanding. Are those really interchangeable?
I’ve reduced this down to its bare minimum, but this particular “question” is disproportionately likely to appear in “comment rather than a question” format.