Inquiry and Community with Collaborative Grading
How collaborative grading helped refocus students and build community

Today’s guest post is brought to you by Jennifer Beichman, who is a senior lecturer in the Department of Mathematical Sciences at Smith College in western Massachusetts. She regularly teaches and coordinates courses in the introductory sequence of Calculus 1 and 2, as well as courses in her areas of specialty: partial differential equations and mathematical analysis. Before coming to Smith in 2016, Beichman was a postdoctoral scholar at the University of Wisconsin-Madison. She completed her Ph.D. in mathematics at the University of Michigan in dispersive differential equations, fluid mechanics and harmonic analysis. When she is not teaching mathematics and advising students, she is finding ways to make things with her hands, ideally with her family - cooking, baking, knitting, or making pottery.
I teach at Smith College, a liberal arts college in western Massachusetts with an undergraduate population of about 2500 students. Smith is a women’s college and about half of the undergraduates major in the natural sciences and mathematics. The mathematics department graduates about 25 each year in the major, but the total number of students we teach is much higher because many majors on campus require calculus.
The class I am writing about today is Introductory Analysis, which sits right in the upper middle of the major requirements - it’s taken after introduction to proof writing, and it is one of the core classes in the major, because of content and because it helps students advance their deductive reasoning and proof-writing skills. Not only mathematics majors but also students interested in graduate school in statistics or economics take the class prior to graduate school. As a result of our growing statistical and data science program, we have had two sections of the course per year in the fall semester for the past five years, running around 12-20 students per section.
At Smith, we teach introductory analysis using inquiry-based learning (IBL).1 “Introductory analysis” usually covers the theory of real numbers and the behavior of functions on the real numbers. If you’ve ever pondered why there are more real numbers than rational numbers (and what “more” even means), this class is for you! In IBL, instead of faculty lecturing, students read lists of definitions on their own, then work in groups on a selection of problems, with one problem assigned per group. On a three-day-a-week schedule, each week becomes a cycle with two days in class for working with their groups and consulting with the professor on their assigned problem, and the third day for presenting their proofs. In essence, students construct all the knowledge in the class collectively and gain understanding and ownership of the material.
When I arrived in 2016, I immediately knew I wanted to teach introductory analysis. I love this branch of mathematics and it was an exciting new teaching method for me. It took several years for my turn to arrive, and as I waited, I learned more about the class from the perspective of students. The consensus was that the class was really hard, people had no idea what they were doing or why, and they never had any idea how they were doing in the class or if they even understood the material. Now, students are not the best sources of information, but the sheer number of students, even strong, graduate-school-bound students, made me think there was something that needed attention.
When I was assigned to teach analysis in Fall 2022, I knew that summer would be focused on keeping what worked in the course but making sure it aligned with my values and goals as an instructor. I tried to identify why students were not connecting with the course the way I hoped they would. I put myself back in time, back when I was a student not understanding things, and I remembered the way I always described working on my dissertation to non-grad students and non-mathematicians: “My advisor told me there is some wonderful treasure deep in this impenetrable jungle. She handed me a machete, a map that is for a different but similar forest, and told me to check in every couple of weeks and let her know what I’ve found.”
Many of you reading probably resonated with that and maybe even got a little burst of excitement thinking about the joy of discovery. Inquiry-based mathematics education taps into that same sense of independent discovery. Of course, undergraduate students who haven’t even (metaphorically) waded into waist-deep grass near their own homes would find charging off into uncharted wilderness all alone pretty anxiety-inducing. When I was preparing for the course, I knew my guiding question would be: How can I keep the inquiry structure while empowering students instead of discouraging them?
(Re)Building the Course
I started just by talking to a lot of people: colleagues in math at Smith, colleagues at Smith in other departments, colleagues in math at other institutions, and my mom.2 Here I need to give special credit to the OPEN Math Inquiry and Inclusion workshop3 for giving me a group of people to inspire me, bounce ideas off of, and give me a collaborative space to think about this course.
All those conversations led me to three fundamental principles to build my course around. Students should:
Feel ownership of the material and their learning,
See measurable, incremental progress, and
Have clear expectations of their deliverables each cycle.
You’ll notice none of these have anything to do with the specific content of my class. The trick in implementation for me was aligning these goals with the inquiry structure and the content of the course, most of which is more theoretical than any other material the students have grappled with up to that point.
In previous semesters, the graded components of the course were written proofs, presentations, and two take-home exams (midterm and final). Written proofs and oral presentations were graded from 0-20, with the proof grade counting the same for everyone in a group, but the presentation grade assigned individually. The two exams counted for the bulk of the final course grade totaling ~50%, the written work was about a third, and the presentations and participation counted for the remainder.
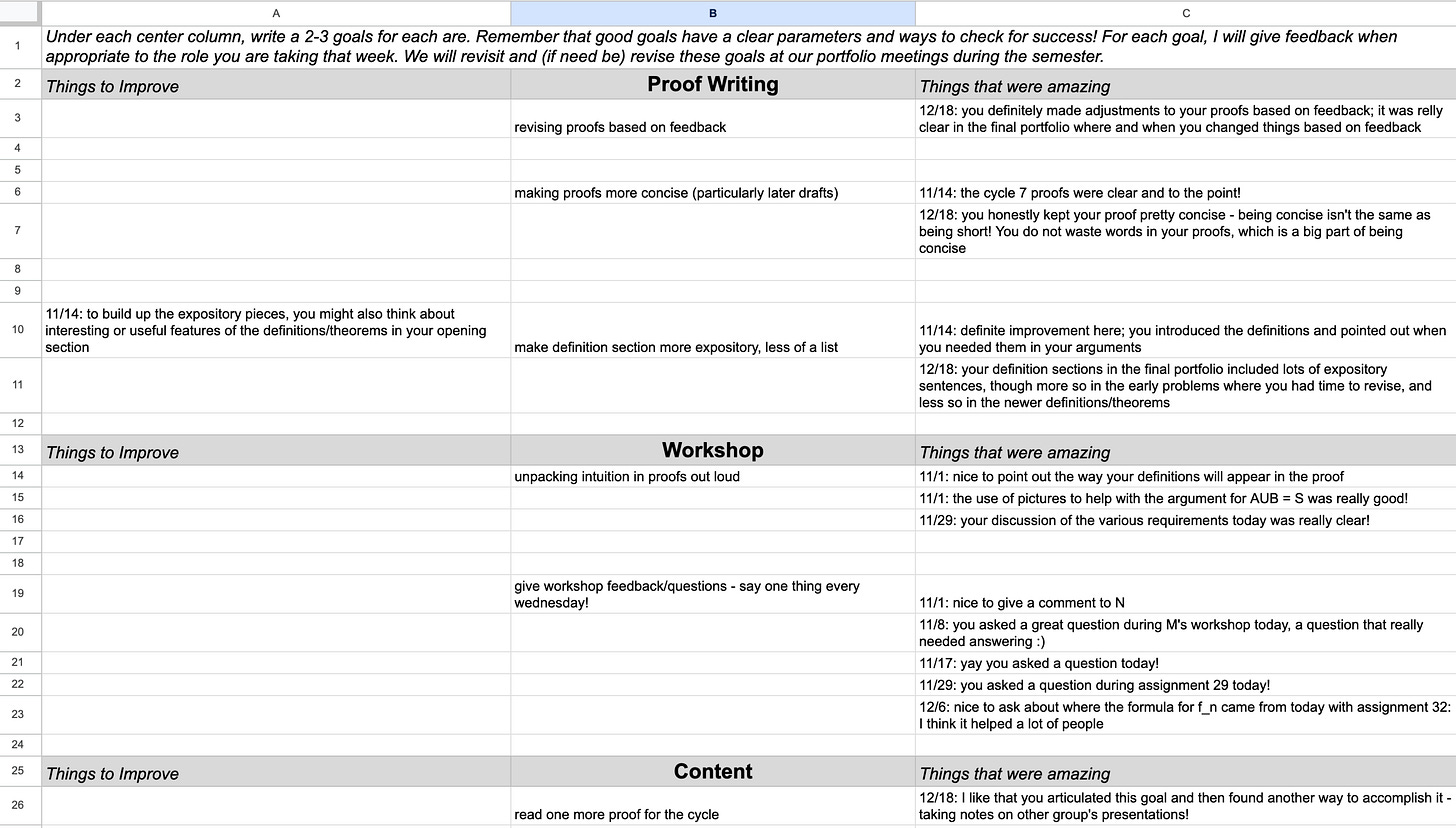
I wanted to encourage student ownership of knowledge. I already have the knowledge, and if I also have control of their grade, there’s a huge asymmetry in classroom power. I decided if I truly wanted to decentralize my authority, I needed to do it completely, which led me to collaborative grading. At the beginning of the semester, I met with each student to articulate goals around writing, workshop, and content/group work. The goals tended to be both general and specific: they want to include different styles of proofs in their portfolio, revise a proof (some for the first time ever), improve their expository writing, get better at starting a problem, give more intuition when discussing proofs, and many, many more. We stored these goals in a shared spreadsheet as one point rubrics that I could update with my comments, and which gave the student space to reflect as well.
We met at least once more during the semester after the student had generated more work for us to discuss to update their goals, if needed. At the end of the semester, I met with each student individually to talk through the whole course. They proposed a grade based on the final version of their portfolio and the feedback I gave them during the semester and each of our one-on-one meetings. The first time through, I took the radical approach of not arguing with them about their grades at all, even if I disagreed with them. The second time, I made sure to ask them to argue clearly for their final course grade in the context of the goals they articulated at the beginning of the semester.
One main advantage for me was that I no longer needed to assign points to proofs. Bad proofs are easy to grade - there is some logical flaw that needs correction. Great proofs are also easy to grade - they flow, the ideas are clear, and nothing extraneous distracts the reader. The stuff in the middle? It just needs revision to move closer to ‘great.’ I wanted to encourage revisions and incremental improvement. Collaborative grading with initial individual goal-setting, specific to the student and where they are at the start of the semester and where they want to go, ticked all these boxes for me.
Supporting and encouraging revision was my method to help students see their progress. Often in math courses, students work on a problem set, get the graded problem set back, and never think about those problems again. I wanted to have revising proofs (over and over again, if necessary) be at the center of student work. To encourage this, I made a simple cosmetic change - instead of having students give presentations, the last day of the cycle became ‘Workshop Day’ where students would talk through in front of the whole class whatever they had so far and then ask for feedback and answer questions. This last day of the cycle was no longer the end of the cycle, but a checkpoint for the whole class to see what everyone was doing. Most of the time, students had a complete proof to present and did not need to ‘workshop’ their solutions, but the name change gave students permission to have incomplete answers and removed some anxiety.
To build up a body of work and see their progress, students generated proof portfolios during the semester. Students turned in portfolios of all their work as a scribe (which I’ll explain below) plus additional problems of their choosing from a list of portfolio problems in Week 5 (2-4 problems total), Week 9 (4-6 problems total), and at the end of the semester (6-8 problems total). The portfolios were cumulative, with each subsequent portfolio containing the same problems (revised as needed) from the previous plus at least two more.
To clarify expectations for students, I leaned into my own penchant for structure. I used group roles to communicate to students their individual expectations in any given cycle. Each group needed to have a scribe to write the proofs, a presenter to lead the workshop, and a manager to organize out of class meetings and keep the group dynamics functioning, and (the second time through) wanderer to look at other groups’ work to get ideas and give feedback. Groups were random and switched every 3-4 cycles, giving everyone in the group a chance with each role.
In order to help students practice the ways the different roles interact and acclimate them to the course structure, I introduced Cycle 0, which consists of material not covered in the original notes and designed as practice for the rhythms of the class. The first time I taught the course, I chose material completely separate from the content of the course to make it clear that Cycle 0 was a practice run, rather than something key to the course. The second time, I changed the content slightly to align more closely with future material, thinking about functions from a set theoretic perspective.
With all these design elements in place, we had a plan for the semester, cycle by cycle. Prior to the start of the cycle, students would read the definitions and complete some prework (a simple Google form). On Day 1, I would start the cycle with a brief (twenty minute) lecture addressing the prework and giving students a chance to ask questions about the definitions before moving into their assigned problem with their group for the remainder of class. Day 2 was all work time; I would provide chalk and white board markers and circulate from group to group asking questions, answering questions, and encouraging students to pursue different ideas. Before Day 3, scribes would post a link to their proof on the class forum, and I (plus any willing peers) would post comments on their draft before workshop day. Day 3 was workshop day, where the presenters from three of the groups (one per problem) would go up and talk through their progress so far. Often, groups working on the same problem would join forces, and if the problem naturally split into parts, each group would take one part, giving more people a chance to workshop. Since the presentations were no longer graded for individual contribution, the number of the people at the board could vary. I found this really helpful since many of my students had never given a math presentation of any kind, and asking for support from their group, another group, anyone in the room, made it less daunting.
Implementation and Future Changes
So how did it go and what tweaking am I still doing? Each semester I’ve taught, the classroom community has grown into something truly remarkable. The students really trust each other and me. Despite huge differences in experience, everyone makes huge strides in their proof writing and reasoning skills. I continue to feel that putting each student on a separate measuring stick is the right method for this course - some students come in loving mathematics and have already watched YouTube videos on cardinality and others have never even thought about the differences between rational numbers and real numbers. And that content is in the first two weeks!
The biggest changes have been in scale - the first time I taught, I had one of the sections and only 14 students. The second time, I taught both offered sections for a total of 37 students. Going from commenting on 4 proofs a week to 10 proofs a week is a big increase, and 37 proof portfolios which needed careful review twice during the semester was a bigger challenge than I expected. Knowing that there would be more to keep track of, I made a centralized tracking spreadsheet4 for me that automatically populated individual student checklists in the same spreadsheet as their individual goals. It was easier to see at a glance what was turned in and what was missing, but tracking down late work (first drafts or second drafts) took a lot more time with a larger collection of students.
There is an underlying tension for me as an instructor with what students know at the end of my class versus what they gain. If I compare the amount of material we cover, it is only a fraction of what I covered in the ten week analysis course that I took as an undergraduate, and I know that many of my students would not be able to complete some of the homework assignments that I did when I learned this material. However, they gain the ability to start from scratch and figure something out working with their peers, to start with a bad proof and revise it to a good one, and to build knowledge rather than regurgitate it. The strength of inquiry based methods in my opinion is the ‘teaching someone to fish’ adage - if a student learns to think, they will always be able to find the knowledge again, whereas if all they learn is to repeat, they won’t be able to find their way back to the process to repeat anyway.
When I reframe the class around students learning the process of understanding definitions and deducing proofs of general principles and theorems, I think the structure and implementation is working well. I still don’t have the best reflection questions, and those will continue to be edited. The addition of the role of wanderer in Fall 2023 did not encourage people to read and comment on other proofs of problems they didn’t work on before workshop day as much as I had hoped. I did realize that the jump from 14 to 37 students made a lot more work for me. For the coming fall, I’m dropping back to teaching only one section plus a section of a different course to diversify my workload and make it easier to stay on top of things.
Overall, I am pleased with the way the course structure and grading scheme because it works for me and for the students. I cannot imagine going back to teaching proof writing without giving opportunities for revisions, and I appreciate that I can focus on the parts of student learning that I find valuable. Removing points and turning grading into a conversation took an obstacle out of my way and replaced it with work that I enjoy doing. The more my grading work aligns with my priorities as an educator, the easier it is to motivate myself to grade. I look forward to seeing my students’ work evolve in the context of material that I love.
We’ve been doing it for about thirty years with many different faculty, but it all started with: A Modified Moore Method for Teaching Undergraduate Mathematics. Cohen, D. W. Am. Math. Monthly, 1982.
Not a joke - my mom was a professor of English at a small liberal arts college before she retired. She taught first year composition almost every year she taught. She remains one of my best sources for thinking about writing instruction and supportive revision.
If any summer 2022 participants are reading - hi! I still think really fondly about our work together.